前文介绍了golang实现基本的四中排序，本文带领大家实现堆排序，堆排序是效率很高的算法，通过取出大根堆堆顶元素从而实现排序的算法。该算法以出色的效率著称，时间复杂度为O (nlgn)

堆排序描述

什么是大根堆

1 大根堆是一颗完全二叉树 2 该完全二叉树，根节点一定大于等于其左右子节点，并且大于等于其子树所有节点。

完全二叉树

完全二叉树是相对于满二叉树来讲的，对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

满二叉树：

一棵深度为 k，且有 2k - 1 个节点称之为满二叉树，即每一层上的节点数都是最大节点数。

也就是说完全二叉树可以这么理解，在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树（Complete Binary Tree）

下图就是一个完全二叉树

算法图解

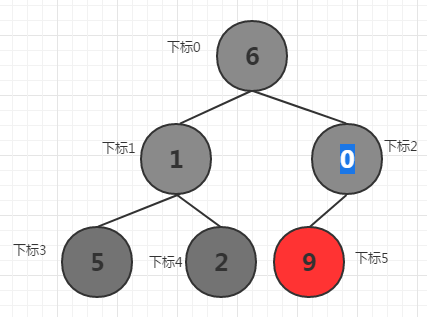
假设有序列下标 | 0 | 1 | 2 | 3 | 4 | 5 | 数值 | 6 | 1 | 0 | 5 | 2 | 9 | 将该序列构造成上图的二叉树，首先从最后一个非叶子结点(也就是下标2的节点元素0)开始，将其所在子树调节为大根堆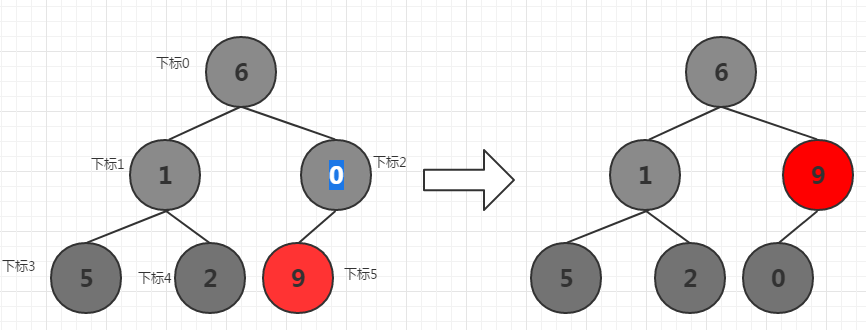由于9比0大，所以二者交换位置，这样下标2所在子树就变为大根堆了。接下来从右往左，从下往上依次处理所有非叶子节点所在子树，使其依次形成大根堆。下面处理下标为1的子树。下标1的两个子节点中5比2大，选择最大的子节点5和1比较，由于5比1大，所以二者交换位置，这样下标1所在子树就变为大根堆了。接下来处理下标0所在子树，使其成为大根堆。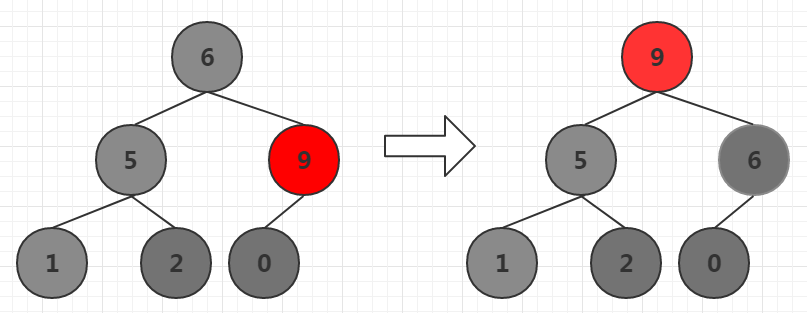同样选择下标0最大的子节点9和下标0的元素6交换位置，这样最大元素9放在下标0的位置，由于6和9交换位置，还要考虑元素6所在的下标为1的子树是否因为交换导致失去大根堆特性，如果6比其子节点小，则继续将6下移，直到找到合理位置。此时6比其子节点0大，所以不需要移动了。下标0就是根节点，到此为止一颗大根堆构造完成。接下来将根节点9和最后一个元素交换，n为最后一个元素。这样调节前n-1节点，是这些节点构成大根堆。具体操作如下图交换最后一个元素和根节点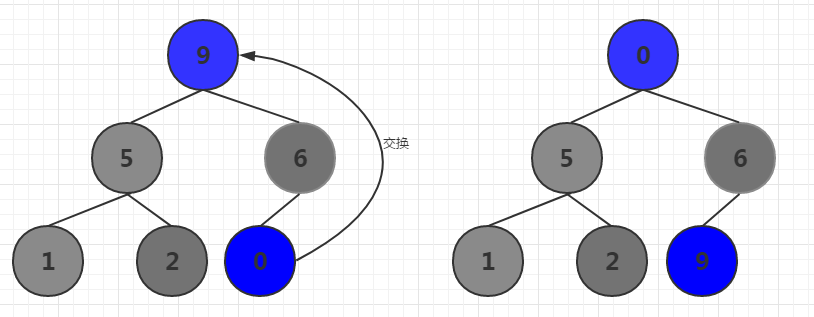将最后一个元素排出不再比较，比较前n-1个元素，重新构造大根堆。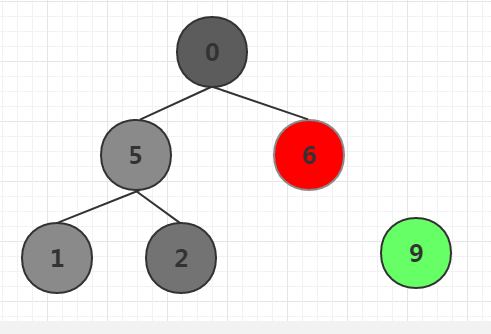以此类推，将n-1个节点调整为大根堆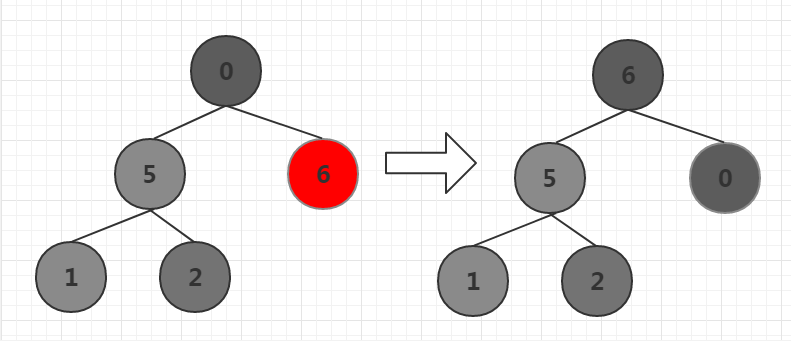前n-1调节为大根堆后，将根元素和第n-1元素交换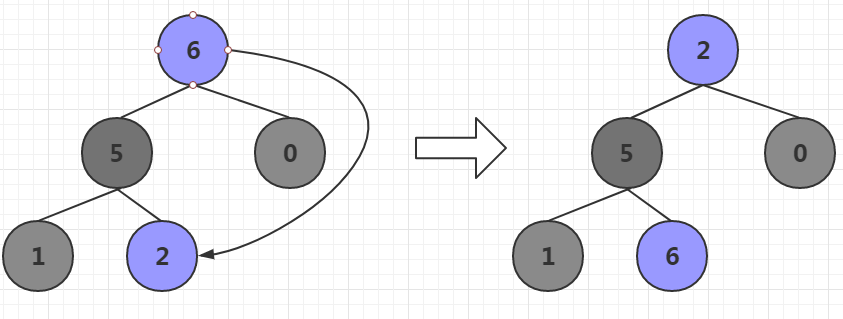将第n-1个元素取出。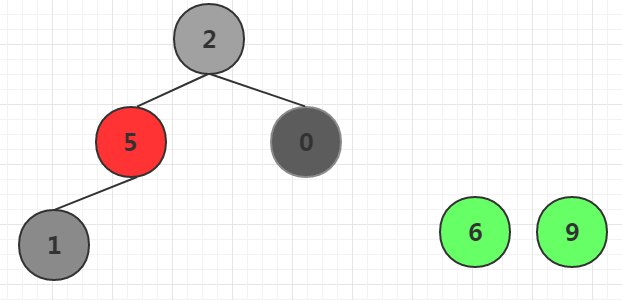这样最后两个元素分别为6,9，是从小到大拍好的顺序，继续使前n-2节点形成大根堆。直到n=1

算法实现

首先定义一个HeapSort类，然后设计一个成员函数adjustHeap，该函数主要实现将index所在位置的子树构造成大根堆。 adjustHeap的三个参数分别为一段连续的数据序列，index表示子树根所在位置，length表示要排序的长度。

type HeapSort struct {
}

//调整index为根的子树，此时index的左右子树都是大根树
//比较index和其左右节点，将index根节点设置为最大的元素
//可能会引起子树失效，所以会循环处理修改的子树
func (hs *HeapSort) adjustHeap(array []int, index, length int) {
    //index 的左右子节点
    leftchild := index*2 + 1
    rightchild := leftchild + 1
    maxchild := leftchild

    for {

        //如果左节点比长度大，说明该节点为子节点
        if leftchild > length-1 {
            break
        }
        //右节点存在，且比左节点大
        if rightchild <= length-1 && array[rightchild] > array[maxchild] {
            maxchild = rightchild
        }
        //index 元素比最大子节点大，则不需要交换，退出
        if array[index] > array[maxchild] {
            break
        }

        //比较自己元素和最大节点的元素，做交换
        hs.swap(array, index, maxchild)
        index = maxchild
        leftchild = index*2 + 1
        rightchild = leftchild + 1
        maxchild = leftchild
    }

}

接下来实现一个小函数，用来交换两个位置的元素

func (hs *HeapSort) swap(array []int, i, j int) {
    if i >= len(array) || j >= len(array) {
        return
    }

    temp := array[i]
    array[i] = array[j]
    array[j] = temp

}

接下来实现将n个元素排序成大根堆，并且交换根元素和第n个元素，并将第n各元素排出，继续比较n-1个元素构造大根堆的逻辑

func (hs *HeapSort) sort(array []int) {

    //每次循环后长度减少，因为每次循环最后元素都变为最大
    for length := len(array); length > 1; length-- {
        //最后一个非叶子节点索引
        lastnode := length/2 - 1
        //从最后一个非叶子节点一次从左到右，从下到上排序子树
        //循环过后得到一个大顶堆(此时还不是大根堆)
        for i := lastnode; i >= 0; i-- {
            hs.adjustHeap(array, i, length)
        }

        //将堆顶元素放到末尾
        hs.swap(array, 0, length-1)
        fmt.Println(array)
    }

}

ok，算法完成，可以进行测试了

func main() {
    //数组初始化
    array := []int{6, 1, 0, 5, 2, 9, 6}
    hs := new(HeapSort)
    hs.sort(array)
}

结果如下，打印的是每次排出元素后序列的结果

[6 5 6 1 2 0 9]
[0 5 6 1 2 6 9]
[2 5 0 1 6 6 9]
[1 2 0 5 6 6 9]
[0 1 2 5 6 6 9]
[0 1 2 5 6 6 9]

目前为止，堆排序介绍完了，欢迎下载源码源码下载地址谢谢关注我的公众号

实现堆排序